概述
首先要明白范式(NF)是什么意思。按照教材中的定义,范式是符合某一种级别的关系模式的集合,表示一个关系内部各属性之间的联系的合理化程度。实际上你可以把它粗略地理解为一张数据表的表结构所符合的某种设计标准的级别。就像家里装修买建材,最环保的是E0级,其次是E1级,还有E2级等等。数据库范式也分为1NF,2NF,3NF,BCNF,4NF,5NF。一般在我们设计关系型数据库的时候,最多考虑到BCNF就够。符合高一级范式的设计,必定符合低一级范式,例如符合2NF的关系模式,必定符合1NF。
同时应用数据库范式可以带来许多好处,但是最重要的好处归结为三点:
- 减少数据冗余(这是最主要的好处,其他好处都是由此而附带的)
- 消除异常(插入异常,更新异常,删除异常)
- 让数据组织的更加准确。
- 但剑是双刃的,应用数据库范式同样也会带来弊端,这会在文章后面说到。
第一范式
1NF的定义为:符合1NF的关系中的每个属性都不可再分
数据库表的每一列都是不可分割的基本数据项,同一列中不能有多个值,即实体中的某个属性不能有多个值或者不能有重复的属性。(保持数据的原子性)
表1所示的情况,就不符合1NF的要求。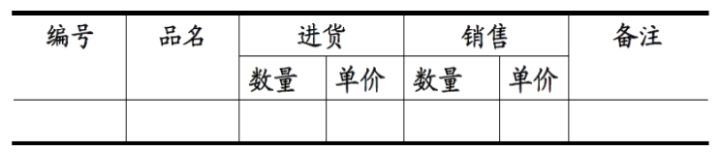
实际上,1NF是所有关系型数据库的最基本要求,你在关系型数据库管理系统(RDBMS),例如SQL Server,Oracle,MySQL中创建数据表的时候,如果数据表的设计不符合这个最基本的要求,那么操作一定是不能成功的。也就是说,只要在RDBMS中已经存在的数据表,一定是符合1NF的。如果我们要在RDBMS存储表中的数据,就得设计为表2的形式:
但是仅仅符合1NF的设计,仍然会存在数据冗余过大,插入异常,删除异常,修改异常的问题,例如对于表3中的设计: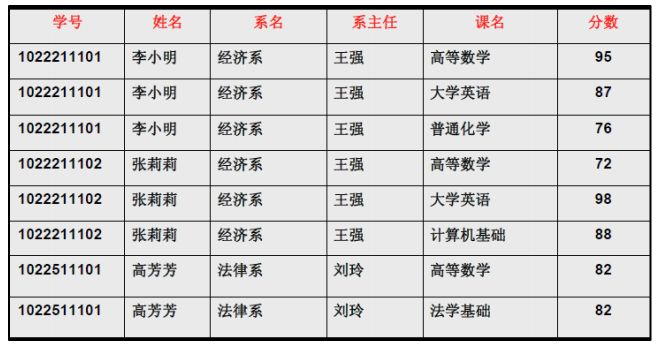
- 数据冗余过大:每一名学生的学号、姓名、系名、系主任这些数据重复多次。每个系与对应的系主任的数据也重复多次
- 插入异常:假如学校新建了一个系,但是暂时还没有招收任何学生(比如3月份就新建了,但要等到8月份才招生),那么是无法将系名与系主任的数据单独地添加到数据表中去的 (注2)
- 注1:码:关系中的某个属性或者某几个属性的组合,用于区分每个元组(可以把元组理解为一张表中的每条记录,也就是每一行)。
- 注2:根据三种关系完整性约束中实体完整性的要求,关系中的码所包含的任意一个属性都不能为空,所有属性的组合也不能重复。为了满足此要求,图中的表,只能将学号与课名的组合作为码,否则就无法唯一地区分每一条记录。
- 删除异常:假如将某个系中所有学生相关的记录都删除,那么所有系与系主任的数据也就随之消失了(一个系所有学生都没有了,并不表示这个系就没有了)。
- 修改异常:假如李小明转系到法律系,那么为了保证数据库中数据的一致性,需要修改三条记录中系与系主任的数据。
正因为仅符合1NF的数据库设计存在着这样那样的问题,我们需要提高设计标准,去掉导致上述四种问题的因素,使其符合更高一级的范式(2NF),这就是所谓的规范化。
第二范式
在满足第一范式的基础上,实体的每个非主键属性完全函数依赖于主键属性(消除部分依赖)
接下来对这句话中涉及到的概念——函数依赖、码、非主属性 进行解释。
函数依赖
若在一张表中,在属性(或属性组)X的值确定的情况下,必定能确定属性Y的值,那么就可以说Y函数依赖于X,写作 X → Y。也就是说,在数据表中,不存在任意两条记录,它们在X属性(或属性组)上的值相同,而在Y属性上的值不同。这也就是函数依赖名字的由来,类似于函数关系 y = f(x),在x的值确定的情况下,y的值一定是确定的。
例如,对于表3中的数据,找不到任何一条记录,它们的学号相同而对应的姓名不同。所以我们可以说姓名函数依赖于学号,写作学号 → 姓名。但是反过来,因为可能出现同名的学生,所以有可能不同的两条学生记录,它们在姓名上的值相同,但对应的学号不同,所以我们不能说学号函数依赖于姓名。表中其他的函数依赖关系还有如:
- 系名 → 系主任
- 学号 → 系主任
- (学号,课名) → 分数
但是以下函数依赖关系则不成立
- 学号->课名
- 学号->分数
- 课名->系主任
从函数依赖这个概念展开,还会有三个概念:
完全函数依赖
在一张表中,如果X->Y,且对于X的任何一个真子集(假如属性组X包含超过一个属性的话,如果是一个那么真子集就是自己),任意真子集用X1表示,X1->Y都不成立,那么我们称Y对于X完全函数依赖,记做:
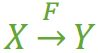
继续用上面表三来做例子:
- 姓名完全依赖于学号
- 分数完全依赖于(学号,课名),(一个学生可能有多门课,因此有多个分数,一个课程有多个学生,就有多个分数)
部分函数依赖:
假如Y函数依赖于X,但同时Y并不完全函数依赖于X。那么我们就称Y部分依赖于X,记作:
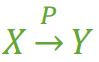
上面定义比较绕,我们可以这样理解,当主键由两个或两个以上字段构成,而表中的某些信息通过主键的一个字段就能唯一确定,我们称这样的依赖关系为部分依赖
比如:
- 姓名完全依赖于(学号,课名),但是学号本身就可以决定姓名。
传递函数依赖
假如Z函数依赖于Y,且Y函数依赖于X ,同时Y不包含于X,且X不函数依赖于Y这个前提,那么我们就称Z传递函数依赖于X ,简单的理解就是A依赖于B,B依赖于C,就可以说A依赖C,记作
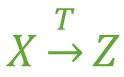
码、候选码和主码
码:简单的说就是能唯一标识实体的属性。如果用前面函数依赖关系来解释,假设K是某表中的一个属性或属性组,若除K之外的所有属性都完全函数依赖于K,那么我们称K为候选码,简称为码。在实际中我们通常可以理解为:假如当 K 确定的情况下,该表除 K 之外的所有属性的值也就随之确定,那么K就是码。
一张表中可以有超过一个码。(实际应用中为了方便,通常选择其中的一个码作为主码)主码我们在建立数据库的时候,需要为每张表指定一个主码,主码也叫主键。所谓主码就是在实体集中区分不同实体的候选码。
例如:在学生实体中,“学号”是能唯一的区分学生实体的,同时又假设“姓名”、“年龄”的属性组合足以区分学生实体,那么{学号}和{姓名,年龄}都是候选码。而我们选择学号极少变化,比较稳定,因此我们选他做主码。
主属性与非主属性
主属性:包含在任一候选码中的属性称主属性。
非主属性 不包含在候选码中的属性称为非主属性。
非主属性是相对与主属性来定义的。
例如:在关系——学生(学号,姓名,年龄,性别,班级)中,
主码是“学号”,那么其他的“姓名”、“年龄”、“性别”、“班级”就都可以称为非主属性
判断表是否符合2NF
接着以上面的表3来举例,看看表3符合第二范式吗?判断的依据实际上就是看数据表中是否存在非主属性对于码的部分函数依赖。若存在,则数据表最高只符合1NF的要求,若不存在,则符合2NF的要求。判断的方法是:
第一步:找出数据表中所有的码。
第二步:根据第一步所得到的码,找出所有的主属性。
第三步:数据表中,除去所有的主属性,剩下的就都是非主属性了。
第四步:查看是否存在非主属性对码的部分函数依赖。
下面我们一步步的来看:
第一步:找出数据表中所有的码
- 查看所有每一单个属性,当它的值确定了,是否剩下的所有属性值都能确定。
- 查看所有包含有两个属性的属性组,当它的值确定了,是否剩下的所有属性值都能确定。
- ……
- 查看所有包含了六个属性,也就是所有属性的属性组,当它的值确定了,是否剩下的所有属性值都能确定。
看起来很麻烦是,但是这里有一个诀窍,就是假如A是码,这里的A可能是一个单独属性也可能是多个属性,那么所有包含了A的属性组,如(A,B)、(A,C)、(A,B,C)等等,都不是码了(因为码的要求里有一个“完全函数依赖要求)。
下图是表3中所有的函数依赖关系:
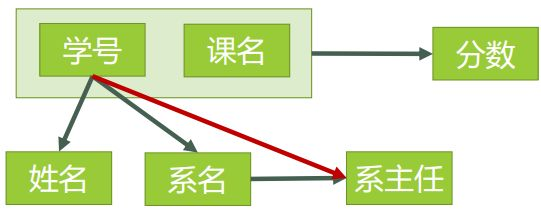
这一步完成以后,可以得到,表3的码只有一个,就是(学号、课名)。
第二步:根据第一步所得到的码,找出所有的主属性
主属性有俩个:学号与课名
第三步:找出所有的非主属性
非主属性有四个:姓名、系名、系主任、分数
第四步:是否存在非主属性对码的部分函数依赖
对于(学号,课名) → 姓名,有 学号 → 姓名,存在非主属性 姓名 对码(学号,课名)的部分函数依赖。
对于(学号,课名) → 系名,有 学号 → 系名,存在非主属性 系名 对码(学号,课名)的部分函数依赖。
对于(学号,课名) → 系主任,有 学号 → 系主任,存在非主属性 对码(学号,课名)的部分函数依赖。
所以表3存在非主属性对于码的部分函数依赖,最高只符合1NF的要求,不符合2NF的要求。
为了让表3符合2NF的要求,我们必须消除这些部分函数依赖,只有一个办法,就是将大数据表拆分成两个或者更多个更小的数据表,在拆分的过程中,要达到更高一级范式的要求,这个过程叫做模式分解。模式分解的方法不是唯一的,以下是其中一种方法:
选课(学号,课名,分数)
学生(学号,姓名,系名,系主任)
我们先来判断以下,选课表与学生表,是否符合了2NF的要求?
对于选课表,其码是(学号,课名),主属性是学号和课名,非主属性是分数,学号确定,并不能唯一确定分数,课名确定,也不能唯一确定分数,所以不存在非主属性分数对于码 (学号,课名)的部分函数依赖,所以此表符合2NF的要求。
对于学生表,其码是学号,主属性是学号,非主属性是姓名、系名和系主任,因为码只有一个属性,所以不可能存在非主属性对于码 的部分函数依赖,所以此表符合2NF的要求。
下表表示了模式分解以后的新的函数依赖关系
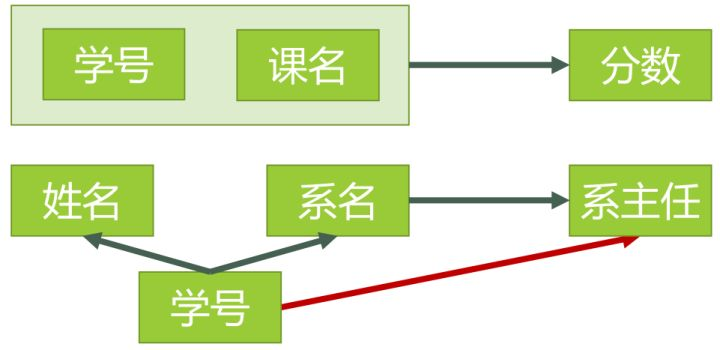
下图是相对应上面表3进行模式分解之后的数据表4图
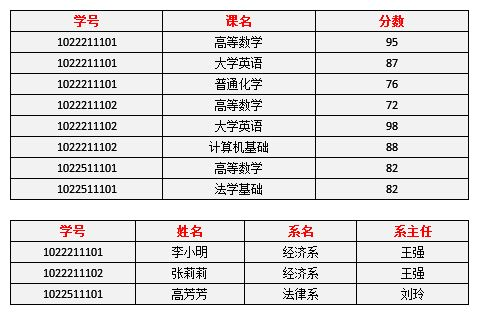
这里来看看相对于上面的第一范式出现的问题,使用上表进行同样的操作,是否还存在问题?
- 数据冗余减少:从上表可以明显的看出,学生的姓名,系主任和系名明显的减少。有改进
- 修改异常:如果李晓明转到法律系,这里只需要修改一条数据。有改进
- 删除异常:删除某个系中所有的学生记录,改系的信息任然全部丢失。无改进。
- 插入异常:插入一个尚无学生的新系的信息,因为学生的学号是主码。不能为空,所以操作不允许。无改进
从上面可以看出,仅仅符合2NF还是不够。在于仍然存在非主属性系主任对于码学号的传递函数依赖。为了能进一步解决这些问题,我们还需要将符合2NF要求的数据表改进为符合3NF的要求。
第三范式
在2NF的基础之上,消除了非主属性对于码的传递函数依赖。
接下来看看我们上面分解出来的表4是否符合3NF的要求:
对于选课表,主码为(学号,课名),主属性为学号和课名,非主属性只有一个,为分数,不可能存在函数传递依赖,所以此表符合3NF。
对于学生表,主码为学号,主属性为学号,非主属性姓名、系名和系主任。因为学号->系名,同时系名->系主任,所以存在非主属性系主任对于主码学号的函数传递依赖,因此学生表不符合3NF。
为了让数据表设计达到3NF,我们必须进一步进行模式分解为以下形式:
选课(学号,课名,分数)
学生(学号,姓名,系名)
系(系名,系主任)
对于选课表,符合3NF的要求,之前已经分析过了。
对于学生表,码为学号,主属性为学号,非主属性为系名,不可能存在非主属性对于码的传递函数依赖,所以符合3NF的要求。
对于系表,码为系名,主属性为系名,非主属性为系主任,不可能存在非主属性对于码的传递函数依赖(至少要有三个属性才可能存在传递函数依赖关系),所以符合3NF的要求。
新的依赖关系如下图:
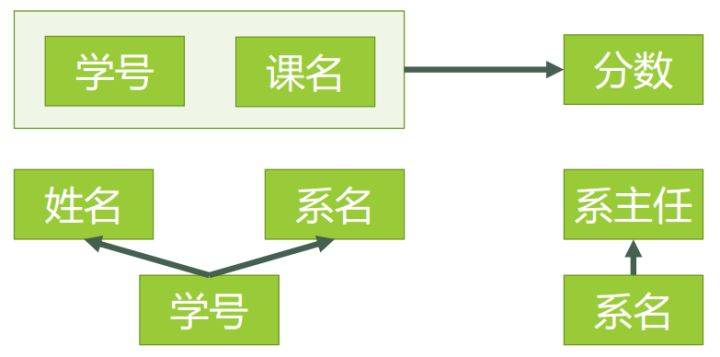
新的数据表如下图
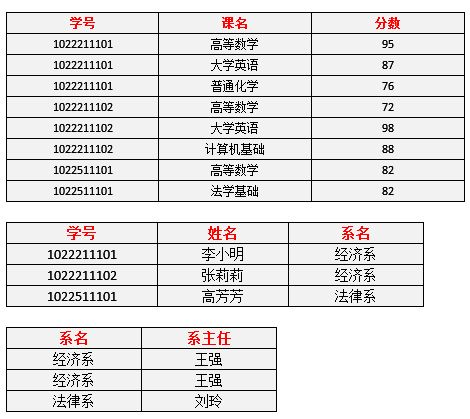
现在我们来看一下,进行同样的操作,是否还存在着之前的那些问题?
- 删除某个系中所有的学生记录
该系的信息不会丢失。——有改进 - 插入一个尚无学生的新系的信息。
因为系表与学生表目前是独立的两张表,所以不影响。——有改进 - 数据冗余更加少了。——有改进
由此可见,符合3NF要求的数据库设计,基本上解决了数据冗余过大,插入异常,修改异常,删除异常的问题。当然,在实际中,往往为了性能上或者应对扩展的需要,经常 做到2NF或者1NF,但是作为数据库设计人员,至少应该知道,3NF的要求是怎样的。
BCNF 范式
要了解 BCNF 范式,那么先看这样一个问题:
- 某公司有若干个仓库;
- 每个仓库只能有一名管理员,一名管理员只能在一个仓库中工作;
- 一个仓库中可以存放多种物品,一种物品也可以存放在不同的仓库中。每种物品在每个仓库中都有对应的数量。
那么关系模式仓库(仓库名,管理员,物品名,数量) 属于哪一级范式?
答:已知函数依赖集:仓库名 → 管理员,管理员 → 仓库名,(仓库名,物品名)→ 数量
码:(管理员,物品名),(仓库名,物品名)
主属性:仓库名、管理员、物品名
非主属性:数量
所以不存在非主属性对码的部分函数依赖和传递函数依赖,此关系模式属于3NF。
基于此关系模式的关系(具体的数据)可能如图所示:
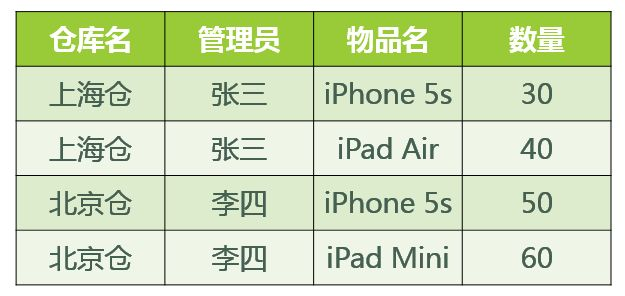
好,既然此关系模式已经属于了 3NF,那么这个关系模式是否存在问题呢?我们来看以下几种操作:
- 先新增加一个仓库,但尚未存放任何物品,是否可以为该仓库指派管理员?——不可以,因为物品名也是主属性,根据实体完整性的要求,主属性不能为空。
- 某仓库被清空后,需要删除所有与这个仓库相关的物品存放记录,会带来什么问题?——仓库本身与管理员的信息也被随之删除了。
- 如果某仓库更换了管理员,会带来什么问题?——这个仓库有几条物品存放记录,就要修改多少次管理员信息。
从这里我们可以得出结论,在某些特殊情况下,即使关系模式符合 3NF 的要求,仍然存在着插入异常,修改异常与删除异常的问题,仍然不是好的设计。
造成此问题的原因:存在着主属性对于码的部分函数依赖与传递函数依赖。(在此例中就是存在主属性【仓库名】对于码【(管理员,物品名)】的部分函数依赖。
解决办法就是要在 3NF 的基础上消除主属性对于码的部分与传递函数依赖。
仓库(仓库名,管理员)
库存(仓库名,物品名,数量)
这样,之前的插入异常,修改异常与删除异常的问题就被解决了。
总结
从上面可以看出,在设计表的时候,通过提高表的数据库范式,可以减少数据冗余,删除异常,插入异常和修改异常。
但是数据库范式越高,则表越多,表多会带来很多问题:
查询时要连接多个表,增加了查询的复杂度
查询时需要连接多个表,降低了数据库查询性能
而现在的情况,磁盘空间成本基本可以忽略不计,所以数据冗余所造成的问题也并不是应用数据库范式的理由。
因此,并不是应用的范式越高越好,要看实际情况而定。