并发队列-无界阻塞队列PriorityBlockingQueue原理研究

概述

PriorityBlockingQueue是带优先级的无界阻塞队列，每次出队都返回优先级最高的元素，是二叉树最小堆的实现，研究过数组方式存放最小堆节点的都知道，直接遍历队列元素是无序的。

简介
源码分析

简介

类图如下

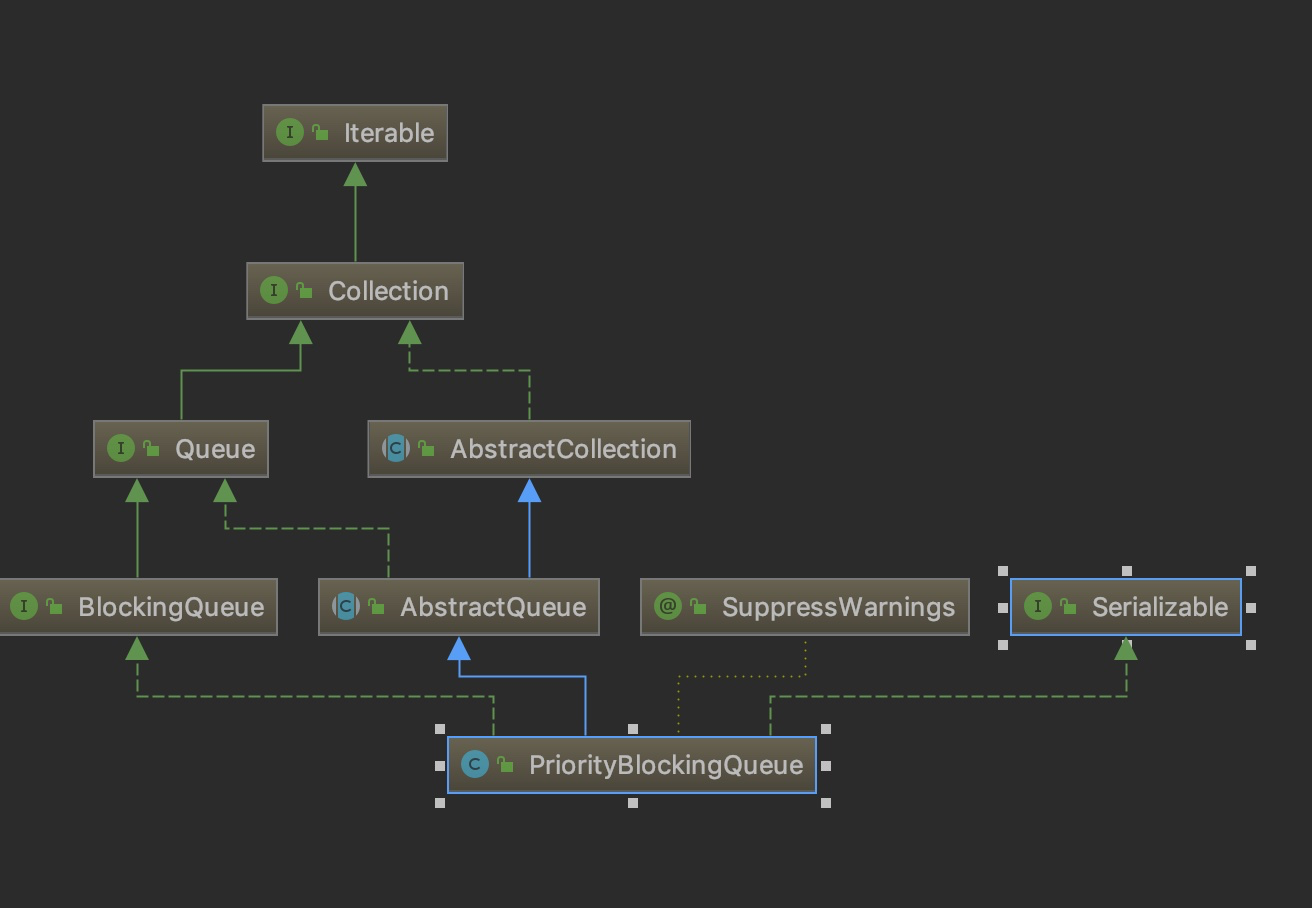
如图PriorityBlockingQueue实现类队列接口，是无界队列的一种。内部其实是通过数组来存放元素的。另外由于这是一个优先级队列所以有个比较器comparator用来比较元素大小。通过全局独占锁对象用来控制同时只能有一个线程可以进行入队出队操作。另外有一点需要特别注意的是：如果没有指定比较器，所有插入的元素都必须实现了比较器接口，否则会抛出异常

源码解析

首先看一下后面要使用到的属性：

// 默认容量
private static final int DEFAULT_INITIAL_CAPACITY = 11;

// 最大数组的分配长度，当超过这个长度可能会抛出OutOfMemoryError
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;

//保存队列的数组
private transient Object[] queue;

// 优先级队列的长度
private transient int size;

// 用于比较优先级的比较器，如果为空则采用自然顺序，也就是从小到大
private transient Comparator<? super E> comparator;

// 全局独占锁
private final ReentrantLock lock;

// 阻塞当队列为空
private final Condition notEmpty;

// 自旋锁，用于数组的扩容，通过CAS来操作
private transient volatile int allocationSpinLock;

构造函数


public PriorityBlockingQueue() {
    this(DEFAULT_INITIAL_CAPACITY, null);
}

public PriorityBlockingQueue(int initialCapacity) {
    this(initialCapacity, null);
}

public PriorityBlockingQueue(int initialCapacity,Comparator<? super E> comparator) {
     if (initialCapacity < 1)
    	 throw new IllegalArgumentException();
     this.lock = new ReentrantLock();
     this.notEmpty = lock.newCondition();
     this.comparator = comparator;
     this.queue = new Object[initialCapacity];
}

入队操作

主要有以下几个方法：

public boolean add(E e)
public boolean offer(E e)
public boolean offer(E e, long timeout, TimeUnit unit)
public void put(E e)

这个几个方法大体上步骤都是一样的，获取锁、入队、释放锁。所有的操作都是调用offer(e)这个操作。其中 offer(E e, long timeout, TimeUnit unit)不会进行阻塞等待，因为他是无界队列所以就没有满的时刻，也就不会发生阻塞等待插入的情况。

下面我们来一起看一下public boolean offer(E e)

public boolean offer(E e) {
    if (e == null)
        throw new NullPointerException();
    final ReentrantLock lock = this.lock;
    lock.lock();
    int n, cap;
    Object[] array;
	// 判断当前数组的的长度是否能够支持这次的入队，不行则需要扩容
    while ((n = size) >= (cap = (array = queue).length))
        tryGrow(array, cap);
    try {
        // 获取比较器
        Comparator<? super E> cmp = comparator;
        // 如果为空，则使用默认的比较器
        if (cmp == null)
            siftUpComparable(n, e, array);
        else
            //使用设置的比较器进行插入
            siftUpUsingComparator(n, e, array, cmp);
        // 队列长度加1
        size = n + 1;
        // 发出队列非空的信号，唤醒正在等待出队的队列
        notEmpty.signal();
    } finally {
        lock.unlock();
    }
    return true;
}

主流程比较简单，下面看看两个主要函数：

private void tryGrow(Object[] array, int oldCap) {
    lock.unlock(); //must release and then re-acquire main lock
    Object[] newArray = null;
 
    //cas成功则扩容
    if (allocationSpinLock == 0 && UNSAFE.compareAndSwapInt(this, allocationSpinLockOffset,0, 1)) {
        try {
            //oldGap<64则扩容新增oldcap+2,否者扩容50%，并且最大为MAX_ARRAY_SIZE
            int newCap = oldCap + ((oldCap < 64) ?
                                   (oldCap + 2) : // grow faster if small
                                   (oldCap >> 1));
            if (newCap - MAX_ARRAY_SIZE > 0) {    // possible overflow
                int minCap = oldCap + 1;
                if (minCap < 0 || minCap > MAX_ARRAY_SIZE)
                    throw new OutOfMemoryError();
                newCap = MAX_ARRAY_SIZE;
            }
            if (newCap > oldCap && queue == array)
                newArray = new Object[newCap];
        } finally {
            allocationSpinLock = 0;
        }
    }
 
    //第一个线程cas成功后，第二个线程会进入这个地方，然后第二个线程让出cpu，
    //尽量让第一个线程执行下面点获取锁，但是这得不到肯定的保证。
    if (newArray == null) // back off if another thread is allocating
        Thread.yield();
    lock.lock();
    // 进行数组的扩容
    if (newArray != null && queue == array) {
        queue = newArray;
        System.arraycopy(array, 0, newArray, 0, oldCap);
    }
}

tryGrow目的是扩容，这里要思考下为啥在扩容前要先释放锁，然后使用cas控制只有一个线程可以扩容成功。我的理解是为了性能，因为扩容时候是需要花时间的，如果这些操作时候还占用锁那么其他线程在这个时候是不能进行出队操作的，也不能进行入队操作，这大大降低了并发性。

所以在扩容前释放锁，这允许其他出队线程可以进行出队操作，但是由于释放了锁，所以也允许在扩容时候进行入队操作，这就会导致多个线程进行扩容会出现问题，所以这里使用了一个spinlock用cas控制只有一个线程可以进行扩容，失败的线程调用Thread.yield()让出cpu，目的意在让扩容线程扩容后优先调用lock.lock重新获取锁，但是这得不到一定的保证，有可能调用Thread.yield()的线程先获取了锁。

那copy元素数据到新数组为啥放到获取锁后面那?原因应该是因为可见性问题，因为queue并没有被volatile修饰。另外有可能在扩容时候进行了出队操作，如果直接拷贝可能看到的数组元素不是最新的。而通过调用Lock后，获取的数组则是最新的，并且在释放锁前数组内容不会变化。

具体的对算法

private static <T> void siftUpComparable(int k, T x, Object[] array) {
    Comparable<? super T> key = (Comparable<? super T>) x;
    // 循环找到合适的位置
    while (k > 0) {
        // 计算父节点位置
        int parent = (k - 1) >>> 1;
        Object e = array[parent];
        // 如果大于父节点，说明找到了合适的位置，则提前结束
        if (key.compareTo((T) e) >= 0)
            break;
        // 将父节点移动合适的位置
        array[k] = e;
        k = parent;
    }
    //插入节点到合适的位置
    array[k] = key;
}

其实就是一个小根堆的实现算法。

出队操作

这里主要介绍poll的实现细节，其他的都差不多

在队列头部获取并移除一个元素，如果队列为空，则返回null

public E poll() {
    final ReentrantLock lock = this.lock;
    lock.lock();   
    try{   
        return dequeue();
    } finally {      
        lock.unlock();   
    }
}

主要看dequeue

private E dequeue() {   
    //队列为空，则返回null
    int n = size - 1;
    if(n < 0)  
        return null;
    else{       
        //获取队头元素(1)
        Object[] array = queue;       
        E result = (E) array[0];
        //获取对尾元素，并值null(2)
        E x = (E) array[n];
        array[n] = null;
        Comparator<? super E> cmp = comparator;
        if(cmp == null)
            //cmp=null则调用这个，把对尾元素位置插入到0位置，并且调整堆为最小堆(3)
            siftDownComparable(0, x, array, n);
        else
            siftDownUsingComparator(0, x, array, n, cmp);
        size = n;
        return result;    
   }
}

调整对的算法

private static <T> void siftDownComparable(int k, T x, Object[] array,
                                            int n) {
     if (n > 0) {
         Comparable<? super T> key = (Comparable<? super T>)x;
         // 计算第最后一个叶节点
         int half = n >>> 1;  
         //  循环直到非页节点
         while (k < half) {
         		// 找到右孩子
             int child = (k << 1) + 1; // assume left child is least
             Object c = array[child];
             int right = child + 1;
             // 比较左右孩子节点，找到相对来说较小的节点
             if (right < n &&
                 ((Comparable<? super T>) c).compareTo((T) array[right]) > 0)(7)
                 c = array[child = right];
              // 结束条件
             if (key.compareTo((T) c) <= 0)
                 break;
             array[k] = c;
             k = child;
         }
         array[k] = key;
     }
 }

上面就是一个小根堆的调整过程

size操作

public int size() {
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        return size;
    } finally {
        lock.unlock();
    }
}

这里返回的是精确的大小

总结

PriorityBlockingQueue类似于ArrayBlockingQueue内部使用一个独占锁来控制同时只有一个线程可以进行入队和出队，另外前者只使用了一个notEmpty条件变量而没有notFull这是因为前者是无界队列，当put时候永远不会处于await所以也不需要被唤醒。

PriorityBlockingQueue始终保证出队的元素是优先级最高的元素，并且可以定制优先级的规则，内部通过使用一个二叉树最小堆算法来维护内部数组，这个数组是可扩容的，当当前元素个数>=最大容量时候会通过算法扩容。

值得注意的是为了避免在扩容操作时候其他线程不能进行出队操作，实现上使用了先释放锁，然后通过cas保证同时只有一个线程可以扩容成功。

参考

并发队列 – 无界阻塞优先级队列 PriorityBlockingQueue 原理探究