最近在看机器学习方面内容，所以需要写一些代码来跑机器学习中一些简单的算法。很多算法都用到numpy这个库。但是对立面axis轴这个名词一直不懂。本篇文章就是来解释这个名词是什么意思。
要想理解这个名词，我们先看一些例子，看懂例子之后，这个名词就比较好理解。
首先我们来看一个
举个例子，现在我们有一个矩阵：
，在 Python，或说在numpy里面，这个矩阵是这样被表达出来的：x = [ [0, 1], [2, 3] ]，然后axis的对应方式就是：
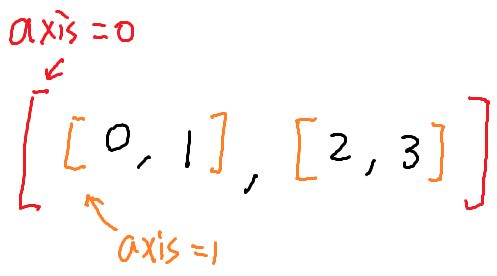
下面我们接着以上面的矩阵来举例子，看看numpy库中sum这个函数，这个函数接收一个参数axis，下面我们分别以axis=0和axis=1来使用这个函数，并解释对应的计算。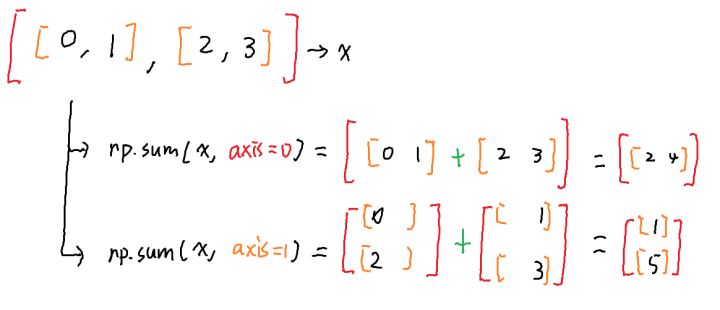
上面图中对应的代码如下：
1 | import numpy as np |
得到的结果如下：
1 | axis 0 |
可以看到，貌似出来的结果比我们推导的结果的括号要少一些。这是因为诸如 np.sum 这种函数中有一个参数叫 keepdims，它的默认值是 False，此时它会把多余的括号给删掉。假如我们把它设为 True 的话，就可以得到和推导中一致的结果了：
1 | import numpy as np |
得到的结果如下
1 | ``` |
下面来看一个更“高维”一点的例子：
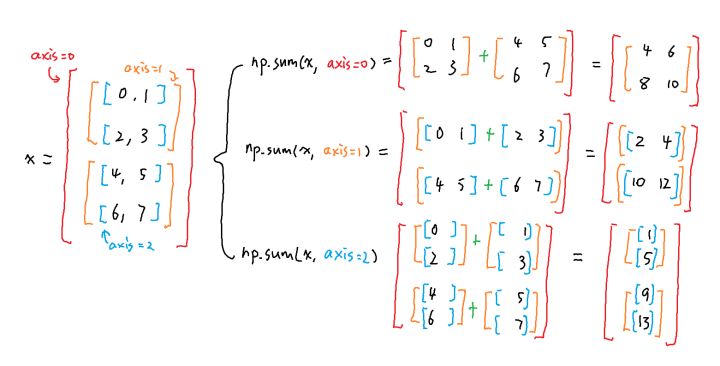
对应的代码实现和运行结果如下：
以及
可以看到结果和我们推导的确实一样
现在我们知道哪个axis对应于数组中的哪些元素了，接下来还需要知道的就是transpose这个函数到底在背后干了什么。从纸面上来看，如果一个高维数组x的shape是 (2, 3, 4)，那么 transpose的作用就是把这个shape 各个数的顺序改一改。比如说：
但是transpose返回的结果究竟是如何得到的，可能就比较难理解了。幸运的是，这个回答非常好地阐明了这背后的原理。
首先是对这个 shape 的理解。直观地说，shape中的各个数就是对应axis的元素个数。比如说上图中的x，它画出来会是这个样子的：
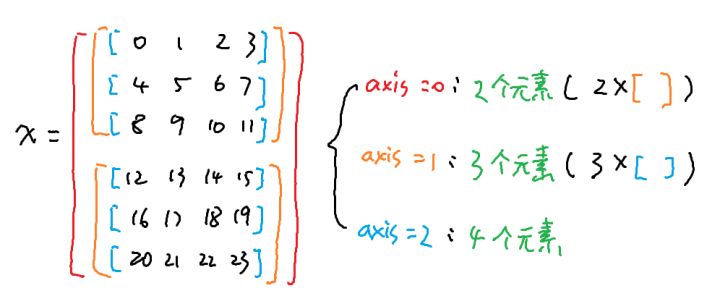
如果我们换一种思路的话，以axis=0为例，由于我们现在整个数组里面一共有24个数，而axis=0 只有两个元素，所以可以理解为在axis=0这个axis上，每隔24/2=12个数就跳一下。比如说上面这个图中就可以看出，两个橙色矩阵对应的数之间差的都是1.2
类似的，由于一个橙色矩阵中只有24 / 2 = 12 个数，所以我们可以理解为在 axis=1 这个 axis 上，每隔 12 / 3 = 4 个数就跳一下。表现在图中，就是同一个橙色矩阵的两个相邻的蓝色向量对应的数之间差的都是 4
再次类似的，由于一个蓝色向量中只有 12 / 3 = 4 个数，我们可以理解为在 axis=2 这个 axis 上，每隔 4 / 4 = 1 个数就跳一下。
所以我们现在可以定义一个新的东西，比如说叫做 strides 吧，它记录着每个 axis 上跳过的数。比如说上图对应的三维数组，它的 strides 就是 (12, 4, 1)
那么接下来激动人心的时刻到了：transpose 的本质，其实就是对 strides 中各个数的顺序进行调换。举个例子：
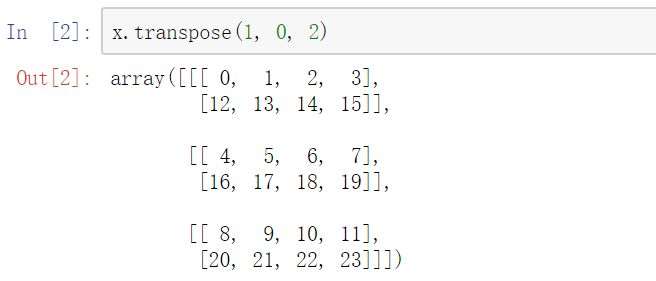
在 transpose(1, 0, 2) 后，相应的 strides 会变成 (4, 12, 1)。而从上图可以看出，transpose 的结果确实满足：
axis=0 的 axis 上，每隔 4 个数跳一下
axis=1 的 axis 上，每隔 12 个数跳一下
axis=2 的 axis 上，每隔 1 个数跳一下
## 参考
1. [Python · numpy · axis](https://zhuanlan.zhihu.com/p/30960190)